McSplit Maximum Common Subgraph Algorithm
Introduction
Maximum common subgraph (MCS) isomorphism algorithms play an important role in chemoinformatics by providing an effective mechanism for the alignment of pairs of chemical structures. It has many chemoinformatics applications, such as, identifying chemical reaction sites (reaction atom mapping), bioactivity prediction of compounds, and exploring structure-activity relationships. Except chemoinformatics, MCS algorithms are used in many other disciplines, and many different MCS algorithms have been developed, but due to the complexity of MCS problems(NP-hard), there is no an effective MCS algorithm until now.
Maximum common subgraph
Before introduce the McSplit algorithm, I must describe some basic definitions.
Induced subgraph of a graph is another graph, formed from a subset of the vertices of the graph and all of the edges (from the original graph) connecting pairs of vertices in that subset. It means for each pair of vertices, if it have an edge in original graph, this edge must be also the induced graph.
Edge-induced subgraph is a set of edges taken from the original graph, in which vertices connected to the edges are included.
A subgraph is a common subgraph of graphs G and H if it is isomorphic to the subgraphs G' and H' of G and H respectively.
There are types of Maximum Common Subgraph. The Maximum Common Induced Subgraph (MCIS) is the largest (in terms of the number of vertices) induced subgraph common to G and H, whereas the Maximum Common Edge Subgraph (MCES) is to find a graph with as many edges as possible that is isomorphic to a subgraph of G and to a subgraph of H simultaneously. These subgraphs are not required to be induced; that is, there can be edges present in either input graph that are not present in the subgraph. There are two types of MCES: the connected MCES (cMCES) and the disconnected MCES (dMCES). A cMCES is one in which each constituent vertex is connected by at least one path in the graph, i.e., the MCES consists of a single, connected subgraph; in a dMCES, conversely, this condition does not hold and the MCES can hence contain two or more subgraphs.
McSplit algorithm
McSplit is one of the state of the art MCS algorithms. It is presented in 2017 by McCreesh et al. It is more than an order of magnitude faster than the previous state of the art for unlabelled and undirected MCS instances. It is also extended for labelled graphs. It is a vertex labelling and partitioning based branch and bound algorithm. The key idea is illustrated as below figure.
In the initialization stage, we partition the input graphs vertices into different classes according the vertex label. Then selecting a vertex matched pair into the matching set, and partition other vertices into new classed by the vertex label and adjacence. For example, in the above figure, after selecting the first pair, the vertices are split into two classes, purple color vertices are adjacent to the selected pair, while green color vertices are not adjacent to the selected pair. Then select the next pair vetices from the two graphs with the same class color, and split vertices into new classes.
The algorithm backtracks when the incumbent (the largest mapping found so far) is at least as large as a calculated bound given M and the current labelling. In the selecting next matched pair procedure, McSplit adopts a heuristic that selects node pairs with the largest degree as its policy. Below is the pesudo-code of the McSplit algorithm.

The original McSplit algorithm is used for MCIS, not MCES. However, the MCES better describes the notion of chemical similarity, and finding the MCES is computationally simpler than finding the MCIS. This is because in the former case, one must take into account both vertex and edge labels, rather than just vertex labels as in the MCIS, with the result that the modular product will contain fewer vertices and edges. The problem of identifying the MCIS can be converted to that of identifying the MCES using a theorem due to Whitney and by Nicholson. If want to find the MCES, just need to convert the original graph to line graph, and then perform the algorithm on the line graph. It should be noted that there is one exception to Whitney’s theorem. This is the so-called \(\Delta\) - Y exchange where two different graphs lead to isomorphic edge-graphs and hence to erroneous results for the MCES when translating back from line graphs to the original graphs: however, such results are easy to identify and prune, hence ensuring the identification of the correct MCES.
Conclusion
The MCS is very helpful in chemoinformatics, however, MCS computation is NP-hard, and state-of-the-art exact MCS solvers do not have worst-case time complexity guarantee and cannot handle large graphs in practice. Designing learning based models to find the MCS between two graphs in an approximate yet accurate way while utilizing as few labeled MCS instances as possible remains to be a challenging task. This post introduce the one of the fastest MCS algorithms, McSplit.
References
Planar Chirality
Introduction
Planar chirality is a term used to refer to stereoisomerism resulting from the arrangement of out of plane groups with respect to a plane. A molecule possessing a chiral plane exhibits planar chirality. A chiral plane is not definable as easily as a chiral center or axis. A chiral plane contains as many of the atoms of the molecule as possible. Chirality is due to the fact that at least one ligand (usually more) is not in the chiral plane. Moelcules with planar chirality include ansa compounds, paracyclophanes, metacyclophanes, metallocene and a few trans-cycloalkenes. In the enantiomers, the methylene chain is on either side of the aryl ring or C=C bond. The interconversion between the enantiomers is prevented by the inability of the alicyclic ring, being too small, to swing from one side to the other of the aryl or olefinic plane.
Definition
Chiral molecules have potential plane of symmetry that consist of some atoms. There exist out of plane group perpendicular to the potential plane. One or more substituents destroys the plane of symmetry, perpendicular to the symmetry plane. In the below figure, atoms a, b and x lying in a potential plane, y-z in a plane with atom z orthogonal to the potential plane and substituent Br destroying symmetry plane fall into planar chirality. Implicit in this description is that z is restricted from lying in the plane.
The (R, S) Specification of Planar Chirality
The specification of these compounds is done by application of the following selection rule.
Selection rule: The most preferred atom directly bound to atoms in the chiral plane is selected as the pilot atom (spectator point). It is the first out-of-plane atom linked to the sequence-preferred end of the chiral plane. The sequencing starts with the first in-plane atom directly bound to the pilot atom (the underlined C) and going along the in-plane sequence (marked as a, b, and c) involving the more preferred atom at each branch. The order in which a, b, and c appear when seen from the pilot atom specifies the absolute configuration, i.e., R for clockwise and S for anticlockwise order.
The specification of planar chirality have three steps. First, pilot atom, not in the plane but attached to an atom in the plane on the side of highest priority in the plane e.g.Br. Second, sequence start at the atom in the plane attached to the pilot, follow atoms in the plane towards to the higher priority atoms. Third, view from the pilot atom, if sequence clockwise (R), anticlockwise (S).
Some compounds of planar chirality and their (R, S) specification.
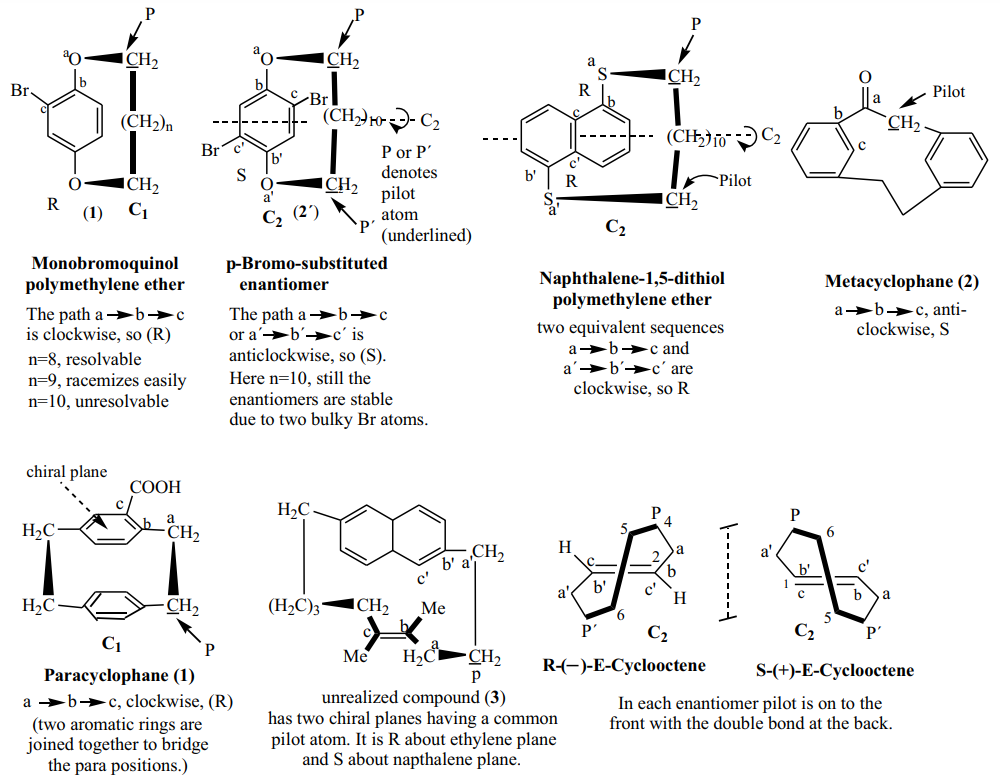
Actually, there are standard CIP nomenclature rules to define the absolute configurations in planar chiral molecules. As described in IUPAC Blue Book 2013. A tetrahedron (tetrahedral stereogenic unit) is derived by connecting the in-plane reference atoms ‘a’ and ‘b’ to the atoms ‘y’ and ‘z’. The chirality sense is determined by conventional rules establishing the priority order ‘a > b > c > d’ or ‘a > b > y > z’ for the cyclophane below. Thus, the descriptor ‘Sp’ is used to denote the configuration and assigned to the carbon atom.
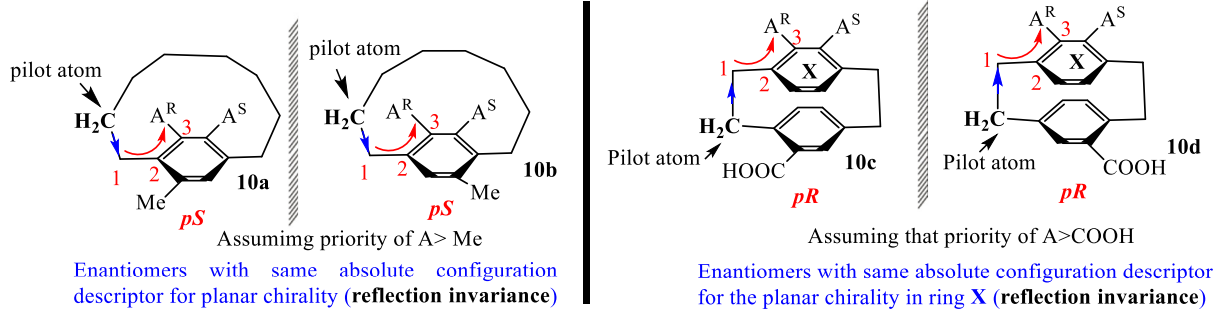
Reflection invariance problems
Since chiral molecules can have two different nonsuperimposable mirror image structures, the 3D-arrangement of groups around a chirality element should have mirror image relationship. The mirror image of R molecule will always be an S molecule. The change of R descriptor to S in the mirror image is called reflection variance (Figure 1) while if R remains R (or S remains S) in the mirror image, that is called reflection invariance. We know that R/S notation are used to assign absolute configuration, so the R form of one enantiomer should become S form in its mirror image. But we can find some special planar chirlaity molecules violate this rule. If two highest ortho substituents are same except configuration on the benzene ring of ansa compounds. When using previous pilot method or standard CIP rule to assign the configuration, reflection invariance is observed.
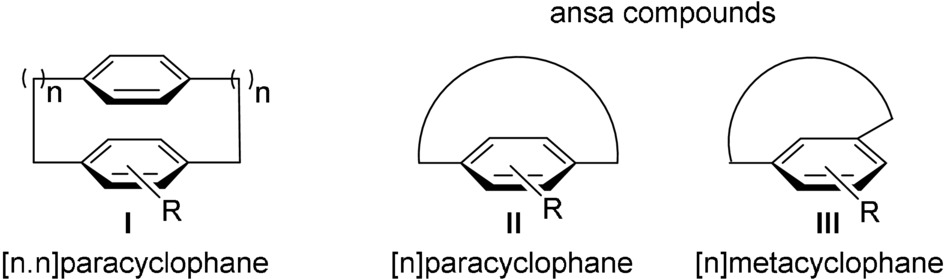
Ansa compounds
Benzene derivatives having para positions (or meta) bridged by a chain (commonly 10 to 12 atoms long) (Latin ansa, handle). By extension, any arene bridged by a chain constrained to lie over one of the two faces of the arene. Generally, there are three types of ansa compounds, [n.n]cyclophanes, [n]cyclophanes and [n]metacyclophane. "Small" cyclophanes with short chains constitute a model for studies on fundamental aspects of strain and aromaticity. The tension imparted on the whole system generates distortion from aromatic planarity and provokes unusual reactivity behaviors. In addition, the restricted rotation of the aromatic ring may generate planar chirality. The configurational stability of this stereogenic unit is hard to predict and relies upon several factors, such as the length and constitution of the chain and the size of the substituents in the aromatic moiety. In contrast to chiral metallocenes and metal arenes, only one substituent is required to produce planar chirality.
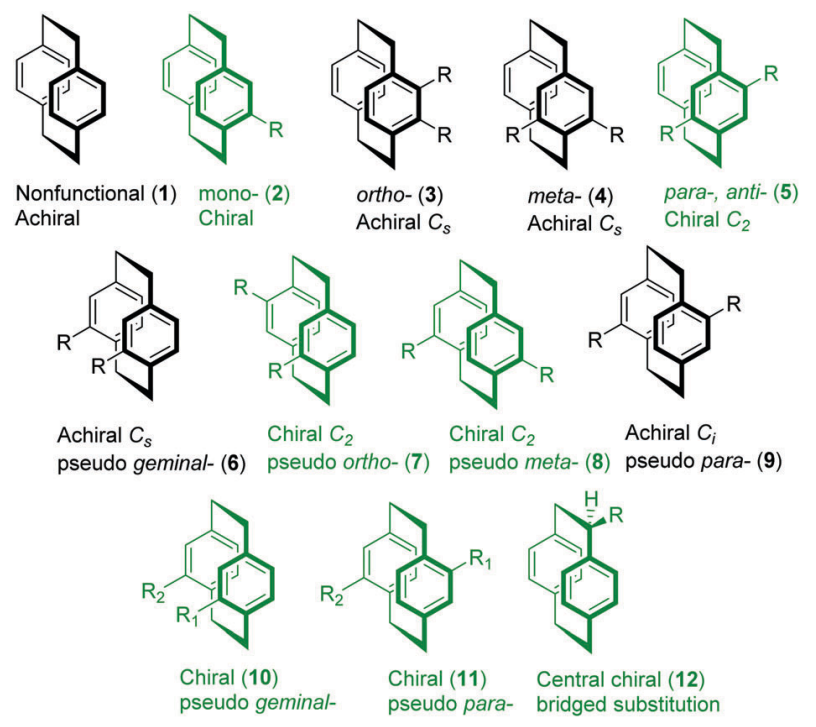
For ansa compounds, the substituents on the benzene ring will affect the planar chirality, if the substituents don't destroy the symmetry plane, they will be achiral. Below figure describe how substituents affect the chirality.
(E)-Cyclooctene
The compound (E)-cyclooctene, which is the first stable cyclic alkene with a trans arrangement of the hydrogen atoms about the double bond. There is a large barrier for the double bond to pass through the ring. Both enantiomers have a two-fold axis of symmetry. Two carbon atoms of the double bond and the directly attached atoms of the substituents (2 carbon and two hydrogen) define the stereogenic plane–the remaining chain can loop around the back from top right to bottom left, or from top left to bottom right. These two forms are enantiomers–remembering that our ultimate criterium for chirality is a mirror image which is not superposable on the original.
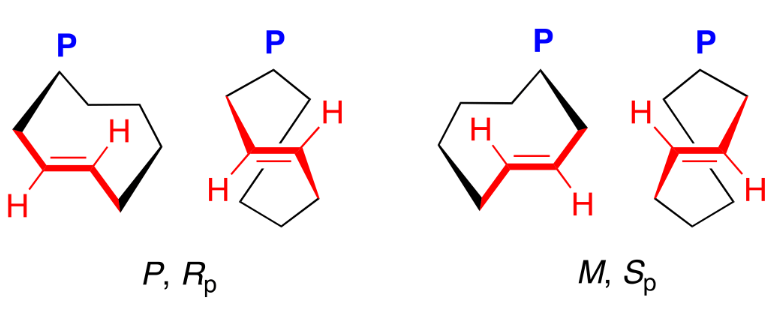
Metallocene
Metallocenes are organometallic coordination compounds in which one atom of a transition metal (iron, ruthenium, manganese, osmium, titanium and zirconium) is bonded to the face of two cyclopentadienyl [η5-(C5H5)] (Cp) ligands which lie in parallel planes.
Planar chirality of metallocenes is related to their threedimensional sandwich-like spatial arrangement where a transition metal is situated between two Cp ligands. Cp anions (Cp−) are achiral flat-shaped chemical species which upon disubstitution (R1 ≠ R2) presents two enantiotopic faces. Thus, π-coordination of the planar prochiral Cp− to a CpM+ (metal cyclopentadienyl cation) discriminates the two enantiotopic faces to induce planar chirality in the metallocene complexes. In other words, disubstitution (in 1,2- or 1,3-positions) of one of the Cp ligands of metallocenes generates a chiral plane (coloured in red) where the two sides of the plane are differently occupied.
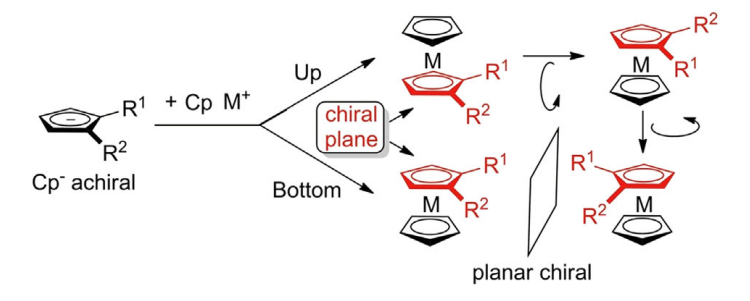
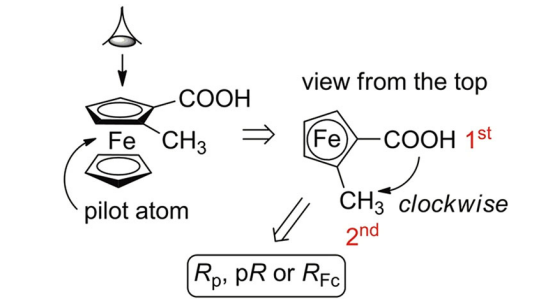
The nomenclature rule proposed by Schlögl in 1964 to define the absolute configuration of planar chiral ferrocene compounds proceeds in three steps. First, considering the chiral plane, iron is assigned as the pilot atom that is the linked atom being out of the chiral plane and with the highest priority based on the CIP priority rules. Second, the chiral plane is observed from the top, thus positioning the iron atom beneath the plane. Third, the two substituents on the Cp are classified according to CIP priority rules: if the relative orientation from the first-priority substituent to the second one is clockwise, the molecule is assigned as an (R)-stereoisomer; if it is counterclockwise, the molecule is assigned as an (S)-stereoisomer.
The standard CIP nomenclature rules generally used for defining absolute configurations of "central chirality" can be applied to the notation of planar-chiral molecules. For example, one can assume that there are virtual σbonds between the central iron atom and each of the five carbon atoms of the cyclopentadienide core in 1-ethyl-2-methylferrocene. With this assumption, the five carbon atoms of the substituted π-ligand can be regarded as "distorted tetrahedral sp3-carbons" which are centrally stereogenic. Then, based on the standard notation method for stereogenic atoms, the five atoms in the planar-chiral ferrocene can be notated either as (R) or as (S). The enantiomer of 1-ethyl-2-methylferrocene is (1S,2R,3R,4S,5S)-isomer. However, this longsome description can be shortened in most cases. Whereas the absolute configurations of the five stereogenic carbon atoms are synchronized each other, the absolute configurations of only the substituted carbon atoms are written as "(1S,2R)-isomer". Occasionally, the absolute configuration of the highest priority atom based on the CIP rules is mentioned and the other's are omitted as "(1S)-isomer" or "(S)-isomer".
As declared above, an identical stereoisomer can be notated either (R)- or (S)-enantiomer depending on the nomenclature rules used. Schlögl, who proposed the former notation rule in 1964, later recommended the use of the latter nomenclature system for planar-chiral compounds. However, two of the pioneering (and still very influential) papers on planar-chiral ferrocenes (Ugi's in 1970; Hayashi & Kumada's in 1974) employed the former nomenclature method, and thus the former rule has been frequently used in metallocene chemistry. On the other hand, the latter notation rule has been popular in (π-arene)chromium chemistry.
Conclusion
Planar chirality is a special class of chirality, this post introduce the classical type of planar chirality, describe the ways to assign the CIP descriptors, and the reflection invariance problems.
References
- Nomenclature of Organic Chemistry. IUPAC Recommendations and Preferred Names 2013.
- Basic Concepts in Organic Stereochemistry
- Ferrocene derivatives with planar chirality and their enantioseparation by liquid‐phase techniques
- Catalytic asymmetric synthesis of planar-chiral transition-metal complexes
- Planar Chirality
- Planar Chirality: A Mine for Catalysis and Structure Discovery
- Planar chiral [2.2]paracyclophanes: from synthetic curiosity to applications in asymmetric synthesis and materials
- Through a Glass Darkly—Some Thoughts on Symmetry and Chemistry
- The reflection invariance problems in stereochemical nomenclature for absolute configuration