Representation and manipulation of stereochemistry

Introduction

A important property of organic compounds is it's stereoisomerism, stereoisomers of the same compound may have very different properties and approximately 50% of marketed drugs are chiral. Representation and manipulation of stereochemistry is a key function of chemoinformatics, and there are many softwares that can handle the stereochemistry. In previous post, I describle the details of CIP priority system. This article presents the details of how to handle the stereochemistry of chemoinformatics softwares.

Cahn-lngold-Prelog Descriptors

Cahn-Ingold-Prelog (CIP) priority system is used for stereochemical naming widely. It associates a label (R, S, r, s, E, Z, M, P, seqCis, seqTrans) with an atom or bond, it is used to code stereochemical information as node and edge attributes added to standard molecule graph. Although the CIP system is widely used, it was found to have the problems for some special case due to it's incompleteness, see previous post. These drawbacks limit it's uses of stereochemistry in computer programs.

Local Descriptors

Chiral features determined through CIP priority system are global chirality, while it is hard to calculate the global feature. And due to the complexity and incompleteness of CIP priority system, it may cause some problems when using global chirality to store the stereochemistry property of compound in chemointormatics softwares.

Local chirality is different from global chirality, it is easy to capture. Local chirality is relevant chiral information of stereogenic unit. For the simplest and most common kind of chirality, tetrahedral; it is defined as; four ligands of stereo atom are renumbered by an arbitrary order, not CIP priority orders, then select the lowest order ligand as observer, and look from the observer to the chiral center, the clockwise/counterclockwise of three other ligands in increasing order. Many system also use two-valued parities (Y/Z, 1/2, +1/-1) to define the configuration of tetrahedral stereocenters. For double bond configuration, it is the opposite/together property of two ending ligands of double bond, in below example, the ligands 1 and 4 are the selected ending ligands, then the local representation is together. The definition of local chirality of tetrahedral and double bond is similar to the representation of chirality in SMILES notation.

The implement of representation of tetrahedral and cis-trans isomerism might look something like this:

public class Tetrahedral
{
    // the stereo atom of stereogenic unit.
	private Atom atom;

    // array to store the ligands of stereo atom, it's size must be four.
	// This representation means that l[1], l[2], and l[3] are ordered 
	// clockwise or counterclockwise when viewed from l[0], along the bond
    // connecting l[0] with the chirality center.
    private Ligand[] ligands;

    // configuration of tetrahedral, clockwise or counterclockwise.
    private Configuration config;
}

public class CisTransIsomerism
{
    // the stereo bond of cis-trans stereogenic unit
	private Bond bond;
	
    // two ending ligands of cis-trans isomerism, it's size must be two.
    private Ligand[] ligands;

    // conformation of cis-trans isomerism, opposite or together.
    private Conformation confor;
}

Comparison with global chirality, if we known constitutional structure of a molecule and local chirality of each atom, it is easy to reconstruct the geometry of the molecule.

Two-valued local parity descriptors defined on the basis of atom numberings are sufficient to describe tetrahedral stereochemistry, because the permutation group of the tetrahedron \(A_4\) has two co-sets in \(S_4\), the symmetric group of four elements and each parity value codes for one of them. \(S_4\) would be the group of allowed ligand permutations of the four ligands of an atom that was configurationally flexible. The configurational constraint restricts the set of equivalent permutations of the nodes of a stereogenic unit to a subgroup.

Calculation of Local Chirality

There are many types of chemical representation, for example SMILES, Mofile, XML. for some types, local chiralities are included in it's content, eg SMILES, it is no need to calculate local chirality, so this section only talk about how to calculation the local chiralities from files with coordinates and bond properties, eg Molfile.

Tetrahedral System

Firstly, let's see the tetrahedral chirality. Stereoisomers with their variety of spatial distribution of differentiated ligands around an asymmetric center can be described – mathematically –using the notion of the space orientation (sign of space), so it is easy to calculate the local chirality using 3D coordinates or 2D coordinates. Sign of space of tetrahedral can be determinated by the fourth grade determinant:

\[ \begin{vmatrix} X_1 & Y_1 & Z_1 & 1 \\ X_2 & Y_2 & Z_2 & 1 \\ X_3 & Y_3 & Z_3 & 1 \\ X_4 & Y_4 & Z_4 & 1 \end{vmatrix} = Z_1 * \begin{vmatrix} X_2 & Y_2 & 1 \\ X_3 & Y_3 & 1 \\ X_4 & Y_4 & 1 \end{vmatrix} - Z_2 * \begin{vmatrix} X_1 & Y_1 & 1 \\ X_3 & Y_3 & 1 \\ X_4 & Y_4 & 1 \end{vmatrix} + Z_3 * \begin{vmatrix} X_1 & Y_1 & 1 \\ X_2 & Y_2 & 1 \\ X_4 & Y_4 & 1 \end{vmatrix} - Z_4 * \begin{vmatrix} X_1 & Y_1 & 1 \\ X_2 & Y_2 & 1 \\ X_3 & Y_3 & 1 \end{vmatrix} \]

Negative values of determinant correspond to the clockwise while a positive one corresponds to counterclockwise.

Cis-Trans Isomerism

It is more easy to figure out the local chirality of cis-trans isomerism than tetrahedral system. Having determined which two ligands attached to atoms that are connected by a double bond are used to calculate the local chirality, one has to find out (calculate) how they are located relative to each other. The double bond is described as opposite if the two ligands lie on opposite sides of the plane of the double bond, or together if the ligands are on the same side of the plane.

Other Stereochemistry Configuration

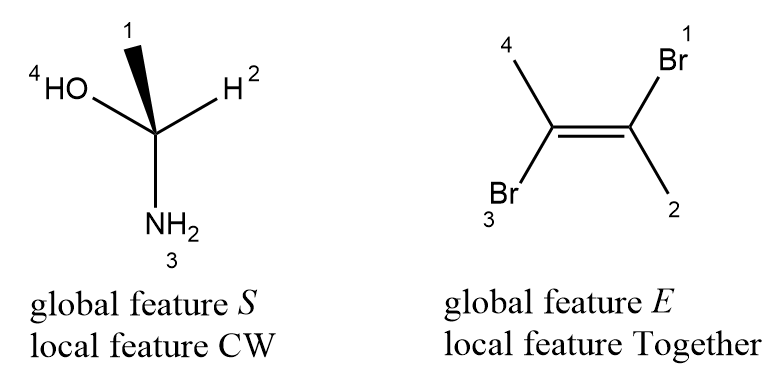
Not only tetrahedral and cis-trans stereochemistry, some other types of stereochemistry also can be represented by local chirality, for example atropisomeric, extended tetrahedral (allenes) and extended cis-trans (odd cumulated double bond) configuration. Method to handle local chirality of atropisomeric and extended tetrahedral configuration is similar the determinant algorithm for tetrahedral configuration ande extended cis-trans is like traditional cis-trans configuration.

A code representation of atropiosmeric configuration may be like this:

public class Atropisomeric
{
    // the link bond of atropiosmeric configuration
	private Bond bond;
	
    // four ligands of atropiosmeric configuration, it's size must be four.
    private Ligand[] ligands;

    // configuration of atropiosmeric configuration, clockwise or counterclockwise.
    private Configuration config;
}

A summary for local representation of stereochemistry is shown below:

Type	Focus	Ligands	Configuration
Tetrahedral	1	2,3,4,5 4,2,5,3	CCW CW
Double Bond	1-2	3,4 3,5	OPPOSITE TOGETHER
Extended Tetrahedral	1	4,5,6,7 6,7,5,4	CCW CW
Extended Cis-Trans	2-3	5,7 6,7	TOGETHER OPPOSITE
Atropisomeric	1-2	3,4,5,6 4,3,5,6	CW CCW

In above figure, for tetrahedral, atropisomeric and extended tetrahedral stereoconfiguration, the configuration is the clockwise/counterclockwise of three other ligands when looking from the first ligand to focus.

Implicit Hydrogen

When drawing chemical structure, it is almost a rule to ignore hydrogen atoms - and later storing in some supported format – the structural diagrams of compounds. The hydrogen atoms are said to be implicit for such compounds. If the atom with implicit hydrogen(s) is an asymmetric center (which is a very frequent case) then additional complexity results for models based on the determinant algorithm. Assignment of ligands for such centers can be a source of additional errors. The situations get even more complicated if one has to handle three-valent nitrogen whose asymmetry is caused by the pair of electrons.

All these problems have nothing to with the determinant algorithm method at all. For implicit hydrogen and nitrogen cases it should be assumed that the coordinates of the missing ligand(s) are identical with the central stereocenter atom and the virtual ligand automatically gets the lowest rank. It can be mathematically proven that such a virtual hydrogen can change the absolute value of the determinant but definitely does not influence the sign of this determinant and thus has meaning in the process of the local configuration detection.

Identification of Global Chirality

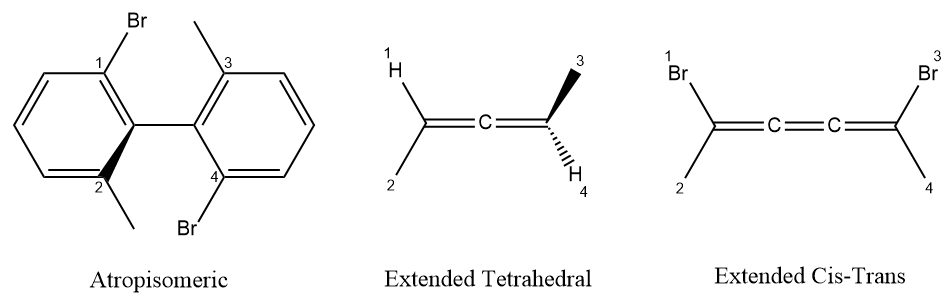
The algorithm that determines the global chirality of a chemical structure based on local chirality is easy to implement. To determine the global chirality according to the R-S notation several steps are needed: (1) indentify the stereocenters, and figure out the local chirality, (2) assign the priority of each ligand according to the CIP rules, (3) determine the parity of the permutation and assign the CIP descriptor.

Tetrahedral System

For tetrahedral stereogenic unit, the identification of a chiral center is based on the properties of atom. After identifying the presence of one or more chiral centers, one must figure out the local chiralities of these chiral centers and classify as clockwise or counterclockwise using the local chirality detection method described in previous section. Then the priorities of ligands attached to the stereocenter are determinated independently according to the CIP rules, for below case the cip priorities are 4 > 3 > 1 > 2. Finally, determining parity of the permutation and assigning the correct CIP descriptor, if the permutation is even, the global feature is equal local feature, else the global feature is the inverted local feature.

Cis-Trans Isomerism

Method to identify the global chirality of cis-trans isomerism is very simple. Following the procedure to determine the E/Z configuration of the two cis-trans stereoisomers, the first step is determining the higher priority substituent on each end of the double bond using CIP priority rules. Then assigning the CIP descriptor according to the priority, if both or neither two ligands of local feature are the higher priority substituent, the final global CIP descriptor is Z, when local feature is together, otherwise the CIP descriptor is E; if either two ligands of local feature if the higher priority substituent, the final global descriptor is Z, when local feature is opposite, otherwise the global descriptor is E.

Stereochemistry Canonicalization

In the chemical database, for the purpose of stereochemically unique representation, the stereochemistry of a structure must be differentiated when processing the structure. There are several classes of algorithm for the stereochemistry canonicalization.

The first class algorithm use stereodescriptors (e.g. CIP descriptors) to designate the absolute configuration of stereocenters of molecule as additional attributes of the graph nodes and edges to further refine the symmetry classes. The algorithms then proceed with the selection of canonical numberings as in the non-stereochemical case. This method works as well as the original stereochemical descriptors describe the structure, but note the problems cited above for the CIP system.

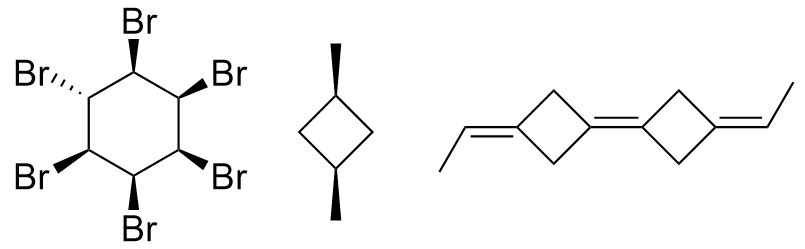
The second class of algorithms uses the ranking of the symmetry classes of the constitutional algorithm to decide which parity symbol to assign to a stereogenic atom or bond. Tetrahedral centers with two ligands in the same symmetry class and double bonds with two equivalent ligands at least on one end are considered non-stereogenic and have their parity removed. The remaining parity symbols are then used as in the previous class to select a canonical numbering. This type of algorithm cannot distinguish ligands of stereocenters or bonds whose dissymmetry originates from their stereochemical structure alone. For standard chiral centers, the atom neighbors should easily be distinguishable during the refinement because they are, by definition, different. However, in the case of dependent chirality, which occurs only for highly symmetric molecules, at least two of the neighbors will seem to be the same. This kind of chirality is determined only by a different constitution of the neighbors, and as indicated by the term “dependent chirality”, at least two chiral centers in the molecule are necessary. bellow are examples of such structures.

The final type of algorithm uses the configurational information during the evaluation of the candidates for the canonical numbering. Some also use them for further refinement of the symmetry classes before actually enumerating candidate assignments. Usually, some coding of the parities of the structure computed from the numbering (or classification) currently considered is used to order the candidate numberings (or classifications) and eventually select the canonical one from a class which creates symmetry equivalent codes. The method for collecting symmetry information during unique numbering mentioned previously has also been used in this case to increase the speed of processing. Only the algorithms of this class compute a provably canonical numbering of the stereochemical connection table given as their input without potential loss of information.

Stereochemical Substructure Search

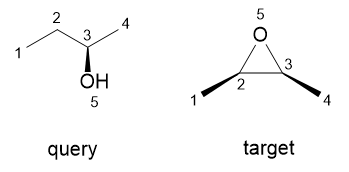
For substructure search, there must be a mapping (a so-called match) of query nodes to target nodes such that node attributes are compatible, atom pairs of bonds in the query map to pairs that are also bonded in the target, and the bond attributes of those bond matches are also compatible. For bellow example, there are two matches, namely {1->1, 2->2, 3->3, 4->4, 5->5} and {1->4, 2->3, 3->2, 4->1, 5->5}. While a stereochemical substructure match must also preserve the stereochemical relationships of the query structure in the matching part of the target. So for stereochemical substructure match, only the second match is correct.

For second match, ligands of query stereocenter 3 (2, 4, 5, H) map to target atom 2 (3, 1, 5, H). If using the above tetrahedral local configuration representation, query is (2, 4, 5, H) -> CW, target is (1, 3, 5, H) -> CCW (the first ligand is the observer, then looking from the observer to the stereocenter, the direction of three other ligands is the local configuration). This quadruple can be converted to the arrangement of the ligands of atom 2 in the target by exchanging 3 with 1, which is an odd number of exchanges, so local configuration for permutation (3, 1, 5, H) is CW, that is matched with query.

For first match, the local configuration of target atom 3 is (2, 4, 5, H) -> CCW. The final mapping is also permutation (2, 4, 5, H), and the final local configuration is CCW. The match is, therefore, stereochemically invalid.

Conclusion

Representation and manipulation of stereochemistry in computer is a key point of chemoinformatics softwares, while how to represent it correctly? Due to the incompleteness of CIP priority system, if using CIP descriptor to represent the chirality, it may cause some problem. Local stereochemistry feature is better way to describe the stereochemistry of molecule, it is easy to calculate, and we can reconstruct the geometry of the molecule of molecule correctly from local stereochemistry feature without loss of stereogenic information. Besides that, after application of CIP priority rules, the global CIP descriptor also can be obtained from local stereo information easily.