Leo He

Representation and manipulation of stereochemistry

Leo He August 29, 2023 / Stereochemistry

Introduction

A important property of organic compounds is it's stereoisomerism, stereoisomers of the same compound may have very different properties and approximately 50% of marketed drugs are chiral. Representation and manipulation of stereochemistry is a key function of chemoinformatics, and there are many softwares that can handle the stereochemistry. In previous post, I describle the details of CIP priority system. This article presents the details of how to handle the stereochemistry of chemoinformatics softwares.

Cahn-lngold-Prelog Descriptors

Cahn-Ingold-Prelog (CIP) priority system is used for stereochemical naming widely. It associates a label (R, S, r, s, E, Z, M, P, seqCis, seqTrans) with an atom or bond, it is used to code stereochemical information as node and edge attributes added to standard molecule graph. Although the CIP system is widely used, it was found to have the problems for some special case due to it's incompleteness, see previous post. These drawbacks limit it's uses of stereochemistry in computer programs.

Local Descriptors

Chiral features determined through CIP priority system are global chirality, while it is hard to calculate the global feature. And due to the complexity and incompleteness of CIP priority system, it may cause some problems when using global chirality to store the stereochemistry property of compound in chemointormatics softwares.

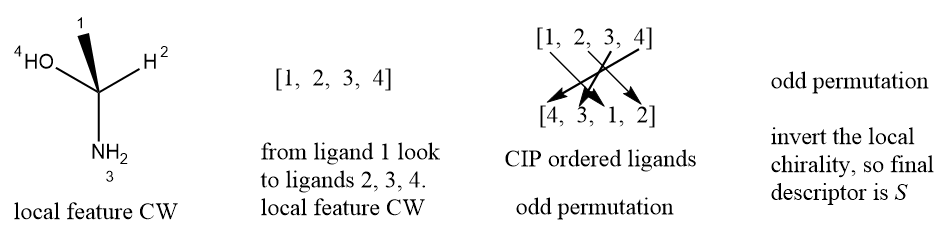
Local chirality is different from global chirality, it is easy to capture. Local chirality is relevant chiral information of stereogenic unit. For the simplest and most common kind of chirality, tetrahedral; it is defined as; four ligands of stereo atom are renumbered by an arbitrary order, not CIP priority orders, then select the lowest order ligand as observer, and look from the observer to the chiral center, the clockwise/counterclockwise of three other ligands in increasing order. Many system also use two-valued parities (Y/Z, 1/2, +1/-1) to define the configuration of tetrahedral stereocenters. For double bond configuration, it is the opposite/together property of two ending ligands of double bond, in below example, the ligands 1 and 4 are the selected ending ligands, then the local representation is together. The definition of local chirality of tetrahedral and double bond is similar to the representation of chirality in SMILES notation.

The implement of representation of tetrahedral and cis-trans isomerism might look something like this:

public class Tetrahedral
{
    // the stereo atom of stereogenic unit.
	private Atom atom;

    // array to store the ligands of stereo atom, it's size must be four.
	// This representation means that l[1], l[2], and l[3] are ordered 
	// clockwise or counterclockwise when viewed from l[0], along the bond
    // connecting l[0] with the chirality center.
    private Ligand[] ligands;

    // configuration of tetrahedral, clockwise or counterclockwise.
    private Configuration config;
}

public class CisTransIsomerism
{
    // the stereo bond of cis-trans stereogenic unit
	private Bond bond;
	
    // two ending ligands of cis-trans isomerism, it's size must be two.
    private Ligand[] ligands;

    // conformation of cis-trans isomerism, opposite or together.
    private Conformation confor;
}

Comparison with global chirality, if we known constitutional structure of a molecule and local chirality of each atom, it is easy to reconstruct the geometry of the molecule.

Two-valued local parity descriptors defined on the basis of atom numberings are sufficient to describe tetrahedral stereochemistry, because the permutation group of the tetrahedron \(A_4\) has two co-sets in \(S_4\), the symmetric group of four elements and each parity value codes for one of them. \(S_4\) would be the group of allowed ligand permutations of the four ligands of an atom that was configurationally flexible. The configurational constraint restricts the set of equivalent permutations of the nodes of a stereogenic unit to a subgroup.

Calculation of Local Chirality

There are many types of chemical representation, for example SMILES, Mofile, XML. for some types, local chiralities are included in it's content, eg SMILES, it is no need to calculate local chirality, so this section only talk about how to calculation the local chiralities from files with coordinates and bond properties, eg Molfile.

Tetrahedral System

Firstly, let's see the tetrahedral chirality. Stereoisomers with their variety of spatial distribution of differentiated ligands around an asymmetric center can be described – mathematically –using the notion of the space orientation (sign of space), so it is easy to calculate the local chirality using 3D coordinates or 2D coordinates. Sign of space of tetrahedral can be determinated by the fourth grade determinant:

\[ \begin{vmatrix} X_1 & Y_1 & Z_1 & 1 \\ X_2 & Y_2 & Z_2 & 1 \\ X_3 & Y_3 & Z_3 & 1 \\ X_4 & Y_4 & Z_4 & 1 \end{vmatrix} = Z_1 * \begin{vmatrix} X_2 & Y_2 & 1 \\ X_3 & Y_3 & 1 \\ X_4 & Y_4 & 1 \end{vmatrix} - Z_2 * \begin{vmatrix} X_1 & Y_1 & 1 \\ X_3 & Y_3 & 1 \\ X_4 & Y_4 & 1 \end{vmatrix} + Z_3 * \begin{vmatrix} X_1 & Y_1 & 1 \\ X_2 & Y_2 & 1 \\ X_4 & Y_4 & 1 \end{vmatrix} - Z_4 * \begin{vmatrix} X_1 & Y_1 & 1 \\ X_2 & Y_2 & 1 \\ X_3 & Y_3 & 1 \end{vmatrix} \]

Negative values of determinant correspond to the clockwise while a positive one corresponds to counterclockwise.

Cis-Trans Isomerism

It is more easy to figure out the local chirality of cis-trans isomerism than tetrahedral system. Having determined which two ligands attached to atoms that are connected by a double bond are used to calculate the local chirality, one has to find out (calculate) how they are located relative to each other. The double bond is described as opposite if the two ligands lie on opposite sides of the plane of the double bond, or together if the ligands are on the same side of the plane.

Other Stereochemistry Configuration

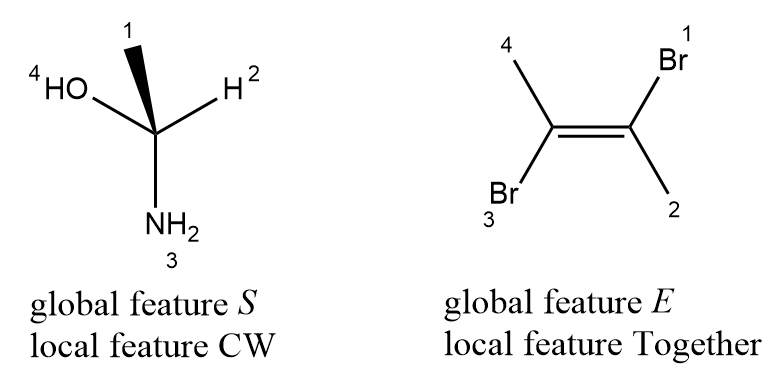
Not only tetrahedral and cis-trans stereochemistry, some other types of stereochemistry also can be represented by local chirality, for example atropisomeric, extended tetrahedral (allenes) and extended cis-trans (odd cumulated double bond) configuration. Method to handle local chirality of atropisomeric and extended tetrahedral configuration is similar the determinant algorithm for tetrahedral configuration ande extended cis-trans is like traditional cis-trans configuration.

A code representation of atropiosmeric configuration may be like this:

public class Atropisomeric
{
    // the link bond of atropiosmeric configuration
	private Bond bond;
	
    // four ligands of atropiosmeric configuration, it's size must be four.
    private Ligand[] ligands;

    // configuration of atropiosmeric configuration, clockwise or counterclockwise.
    private Configuration config;
}

A summary for local representation of stereochemistry is shown below:

Type	Focus	Ligands	Configuration
Tetrahedral	1	2,3,4,5 4,2,5,3	CCW CW
Double Bond	1-2	3,4 3,5	OPPOSITE TOGETHER
Extended Tetrahedral	1	4,5,6,7 6,7,5,4	CCW CW
Extended Cis-Trans	2-3	5,7 6,7	TOGETHER OPPOSITE
Atropisomeric	1-2	3,4,5,6 4,3,5,6	CW CCW

In above figure, for tetrahedral, atropisomeric and extended tetrahedral stereoconfiguration, the configuration is the clockwise/counterclockwise of three other ligands when looking from the first ligand to focus.

Implicit Hydrogen

When drawing chemical structure, it is almost a rule to ignore hydrogen atoms - and later storing in some supported format – the structural diagrams of compounds. The hydrogen atoms are said to be implicit for such compounds. If the atom with implicit hydrogen(s) is an asymmetric center (which is a very frequent case) then additional complexity results for models based on the determinant algorithm. Assignment of ligands for such centers can be a source of additional errors. The situations get even more complicated if one has to handle three-valent nitrogen whose asymmetry is caused by the pair of electrons.

All these problems have nothing to with the determinant algorithm method at all. For implicit hydrogen and nitrogen cases it should be assumed that the coordinates of the missing ligand(s) are identical with the central stereocenter atom and the virtual ligand automatically gets the lowest rank. It can be mathematically proven that such a virtual hydrogen can change the absolute value of the determinant but definitely does not influence the sign of this determinant and thus has meaning in the process of the local configuration detection.

Identification of Global Chirality

The algorithm that determines the global chirality of a chemical structure based on local chirality is easy to implement. To determine the global chirality according to the R-S notation several steps are needed: (1) indentify the stereocenters, and figure out the local chirality, (2) assign the priority of each ligand according to the CIP rules, (3) determine the parity of the permutation and assign the CIP descriptor.

Tetrahedral System

For tetrahedral stereogenic unit, the identification of a chiral center is based on the properties of atom. After identifying the presence of one or more chiral centers, one must figure out the local chiralities of these chiral centers and classify as clockwise or counterclockwise using the local chirality detection method described in previous section. Then the priorities of ligands attached to the stereocenter are determinated independently according to the CIP rules, for below case the cip priorities are 4 > 3 > 1 > 2. Finally, determining parity of the permutation and assigning the correct CIP descriptor, if the permutation is even, the global feature is equal local feature, else the global feature is the inverted local feature.

Cis-Trans Isomerism

Method to identify the global chirality of cis-trans isomerism is very simple. Following the procedure to determine the E/Z configuration of the two cis-trans stereoisomers, the first step is determining the higher priority substituent on each end of the double bond using CIP priority rules. Then assigning the CIP descriptor according to the priority, if both or neither two ligands of local feature are the higher priority substituent, the final global CIP descriptor is Z, when local feature is together, otherwise the CIP descriptor is E; if either two ligands of local feature if the higher priority substituent, the final global descriptor is Z, when local feature is opposite, otherwise the global descriptor is E.

Stereochemistry Canonicalization

In the chemical database, for the purpose of stereochemically unique representation, the stereochemistry of a structure must be differentiated when processing the structure. There are several classes of algorithm for the stereochemistry canonicalization.

The first class algorithm use stereodescriptors (e.g. CIP descriptors) to designate the absolute configuration of stereocenters of molecule as additional attributes of the graph nodes and edges to further refine the symmetry classes. The algorithms then proceed with the selection of canonical numberings as in the non-stereochemical case. This method works as well as the original stereochemical descriptors describe the structure, but note the problems cited above for the CIP system.

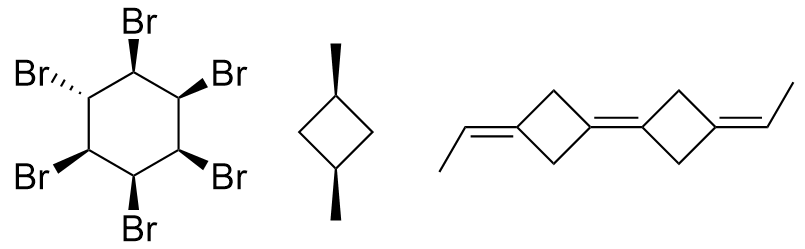
The second class of algorithms uses the ranking of the symmetry classes of the constitutional algorithm to decide which parity symbol to assign to a stereogenic atom or bond. Tetrahedral centers with two ligands in the same symmetry class and double bonds with two equivalent ligands at least on one end are considered non-stereogenic and have their parity removed. The remaining parity symbols are then used as in the previous class to select a canonical numbering. This type of algorithm cannot distinguish ligands of stereocenters or bonds whose dissymmetry originates from their stereochemical structure alone. For standard chiral centers, the atom neighbors should easily be distinguishable during the refinement because they are, by definition, different. However, in the case of dependent chirality, which occurs only for highly symmetric molecules, at least two of the neighbors will seem to be the same. This kind of chirality is determined only by a different constitution of the neighbors, and as indicated by the term “dependent chirality”, at least two chiral centers in the molecule are necessary. bellow are examples of such structures.

The final type of algorithm uses the configurational information during the evaluation of the candidates for the canonical numbering. Some also use them for further refinement of the symmetry classes before actually enumerating candidate assignments. Usually, some coding of the parities of the structure computed from the numbering (or classification) currently considered is used to order the candidate numberings (or classifications) and eventually select the canonical one from a class which creates symmetry equivalent codes. The method for collecting symmetry information during unique numbering mentioned previously has also been used in this case to increase the speed of processing. Only the algorithms of this class compute a provably canonical numbering of the stereochemical connection table given as their input without potential loss of information.

Stereochemical Substructure Search

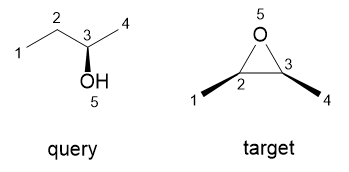
For substructure search, there must be a mapping (a so-called match) of query nodes to target nodes such that node attributes are compatible, atom pairs of bonds in the query map to pairs that are also bonded in the target, and the bond attributes of those bond matches are also compatible. For bellow example, there are two matches, namely {1->1, 2->2, 3->3, 4->4, 5->5} and {1->4, 2->3, 3->2, 4->1, 5->5}. While a stereochemical substructure match must also preserve the stereochemical relationships of the query structure in the matching part of the target. So for stereochemical substructure match, only the second match is correct.

For second match, ligands of query stereocenter 3 (2, 4, 5, H) map to target atom 2 (3, 1, 5, H). If using the above tetrahedral local configuration representation, query is (2, 4, 5, H) -> CW, target is (1, 3, 5, H) -> CCW (the first ligand is the observer, then looking from the observer to the stereocenter, the direction of three other ligands is the local configuration). This quadruple can be converted to the arrangement of the ligands of atom 2 in the target by exchanging 3 with 1, which is an odd number of exchanges, so local configuration for permutation (3, 1, 5, H) is CW, that is matched with query.

For first match, the local configuration of target atom 3 is (2, 4, 5, H) -> CCW. The final mapping is also permutation (2, 4, 5, H), and the final local configuration is CCW. The match is, therefore, stereochemically invalid.

Conclusion

Representation and manipulation of stereochemistry in computer is a key point of chemoinformatics softwares, while how to represent it correctly? Due to the incompleteness of CIP priority system, if using CIP descriptor to represent the chirality, it may cause some problem. Local stereochemistry feature is better way to describe the stereochemistry of molecule, it is easy to calculate, and we can reconstruct the geometry of the molecule of molecule correctly from local stereochemistry feature without loss of stereogenic information. Besides that, after application of CIP priority rules, the global CIP descriptor also can be obtained from local stereo information easily.

References

Cahn-Ingold-Prelog (CIP) Priority System

Leo He August 10, 2023 / Stereochemistry

Introduction

Cahn–Ingold–Prelog (CIP) priority system is used to unambiguously assign the handedness of stereogenic units in organic compounds. The priority of attached ligands is established by the application of ‘Sequence Rules’. It was created by three chemists: R.S. Cahn, C. Ingold, and V. Prelog, the key paper of CIP priority system was published in 1966 and was revised further in later several decades. Now, it was incorporated into the rules of the International Union of Pure and Applied Chemistry (IUPAC) Nomenclature of Organic Chemistry(BB 2013). This post will describe the CIP priority system as much detailed as possible.

Preliminary

Cahn-Ingold-Prelog (CIP) stereodescriptors

‘R’ and ‘S’, to designate the absolute configuration of tetracoordinate (quadriligant) chirality centers;
‘r’ and ‘s’, to designate the absolute configuration of pseudoasymmetric centers;
‘M’ and ‘P’, to specify the absolute configuration of an axial or planar entity using the helicity rule;
‘m’ and ‘p’, to specify the absolute configuration of a pseudoasymmetric entity using the helicity rule;
‘seqCis’ and ‘seqTrans’(some software using z and e), to describe the configuration of enantiomorphic double bonds;
‘seqcis’ and ‘seqtrans’(‘E’='seqtrans' and ‘Z’='seqcis') are used to describe ‘cis/trans-isomers’ at diastereomorphic double bonds.

Capitalized CIP stereodescriptors are variant on reflection in a mirror (i.e. ‘R’ becomes ‘S’ and ‘S’ becomes ‘R’); lower case CIP stereodescriptors are invariant on reflection in a mirror (i.e. ‘r’ remains ‘r’ and ‘s’ remains ‘s’).

The ‘E’ and ‘Z’ stereodescriptors have been classified as non-CIP stereodescriptors. The reason is that they do not distinguish between geometrically diasteromorphic double bonds whose descriptors are reflection invariant (‘common’ double bonds) from the geometrically enantiomorphic double bonds whose stereodescriptors are reflection variant. In the CIP system, reflection variant descriptors are capitalized (for example ‘R’ and ‘S’) and reflection invariant descriptors are lower-case descriptors (for example ‘r’ and ‘s’). The fact that ‘E’ and ‘Z’ are capitalized is contrary to their reflection invariant status. Hirschman and Hanson proposed to use the descriptors ‘seqcis’, ‘seqtrans’, ‘seqCis’, and ‘seqTrans’ as CIP descriptors.

Hierarchical digraphs

In order to establish the order of precedence of ligands in a stereogenic unit, the atoms of the stereogenic unit are rearranged in a hierarchical diagram, called a ‘digraph’ or ‘tree-graph’, representing the connectivity (topology) and make-up of atoms; a digraph originates from the core of the stereogenic unit and is developed by indicating the various branches representing ligands. A digraph must be established for each stereogenic unit generating several digraphs when several stereogenic units are present in a molecule.

Digraph of stereocenter 3.

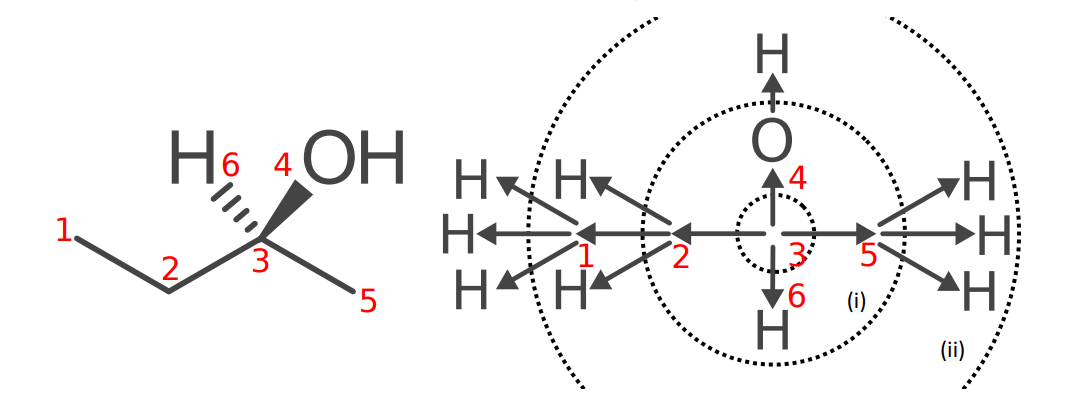
Double and triple bonds

If an atom is double-bonded or triple-bonded to another atom, the double and triple bonds are split into two and three bonds respectively. (C) and (N) are duplicate atom representations of the atoms at the other end of the double or triple bond

Rings and ring systems

To correctly detect CIP, a cyclic molecule must be expanded into an acyclic digraph by traversing bonds in all possible paths starting at the stereocenter. When the traversal encounters an atom through which the current path has already passed, a duplicate atom is generated in order to keep the tree finite. A single atom of the original molecule may appear in many places (some as phantoms, some not) in the tree.

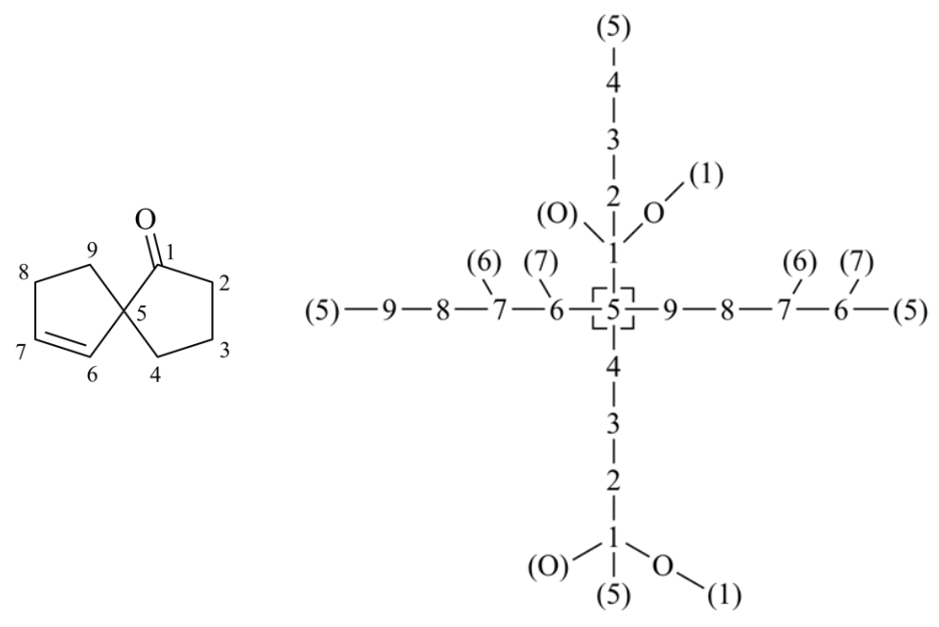
Mancude rings and ring systems

Mancude rings, i.e., rings or ring systems having the maximum number of noncumulative double bonds, are treated as Kekulé structures. For mancude heterocycles, each duplicate atom is given an atomic number that is the mean of what it would have if the double bonds were located at each of the possible positions. For mancude hydrocarbons, it is immaterial which Kekulé structure is used because ‘splitting’ the double bonds gives the same result in all cases. Without averaging the atomic number in Rule 1a, bellow two chemically equivalent Kekulé structures give different descriptor assignments at the stereocenter.

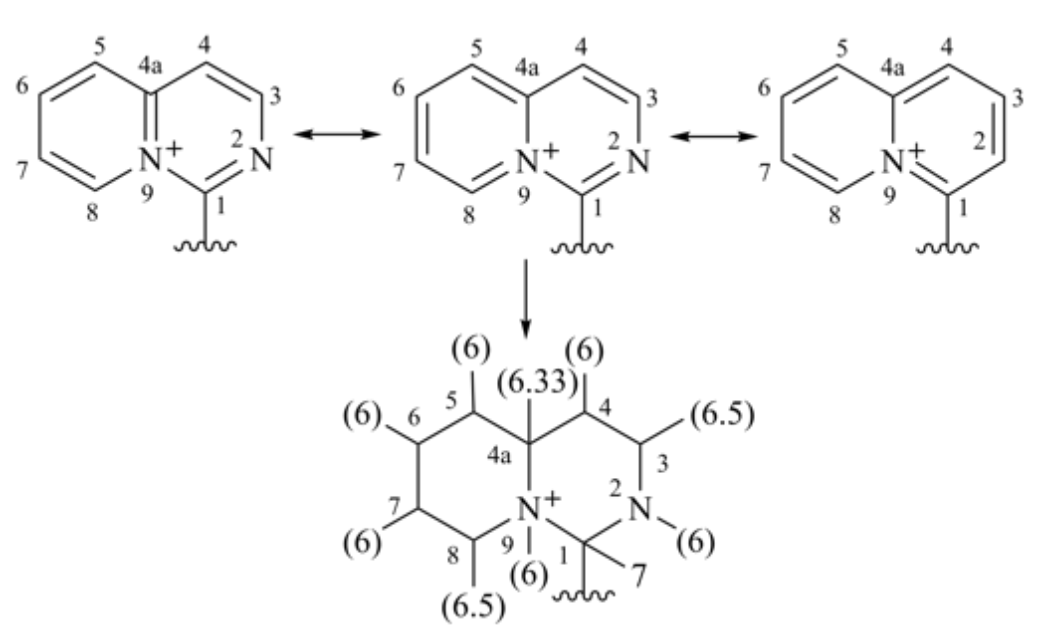
‘C-1’ is doubly bonded to one or the other of the nitrogen atoms and never to carbon, so its added duplicate atom has an atomic number of 7 (that of nitrogen). ‘C-3’ is doubly bonded either to ‘C-4’ (atomic number 6) and to ‘N-2’ (atomic number 7); so its added duplicate atom has an atomic number of 6½, as it is for ‘C-8’. But ‘C-4a’ may be doubly bonded to ‘C-4’, ‘C-5’ and ‘N-9’, so its added duplicate atom has an atomic number of 6⅓

Exploration of a hierarchical digraph

Digraphs are constructed to show the ranking of atoms according to the topological distance i.e., number of bonds, from the core of the stereogenic unit (i.e., center) and their evaluation by the Sequence Rules.

Atoms lie in spheres and atoms of equal distance from the core of the stereogenic unit are in the same sphere; spheres are identified as I, II, III, and IV.
Atoms in the nth sphere have precedence over those in the (n + 1)th sphere.
The ranking of each atom in the nth sphere depends in the first place on the ranking of atoms of the same branch in (n - 1)th sphere, and then the application of the Sequence Rules to it.
Those atoms in the nth sphere which are of equal rank with respect to those in the (n − 1)th sphere in the same branch are ranked by means of the Sequence Rules, first by the exhaustive application of Sequence Rule 1; if no decision is reached, Sequence Rule 2 is exhaustively applied, and so on.

Ranking of ligands: Application of the Sequence Rules

In general, Ligands are ranked sphere by sphere, branch by branch in a breadth-first fashion, Then two ligands are compared atom by atom, in order of that ranking. Sequence rules are applied as follows:

each rule is applied in accordance with a hierachical digraph
each rule is applied exhaustively to all ligands being compared;
the ligand that is found to have precedence (priority) at the first occurrence of a difference in a digraph retains this precedence (priority) regardless of differences that occur later in the exploration of the digraph;
precedence (priority) of an atom in a group established by a rule does not change on application of a subsequent rule.

Auxiliary descriptors

Temporary “auxiliary descriptors” are assigned solely on the basis of a given digraph for a particular stereogenic unit in question and may or may not be the “final” descriptors ultimately used to describe those centers in the end. Below shows an example where only a minority of the auxiliary descriptors are the same as the final descriptors for the corresponding atoms.

It is important to note that full digraphs are necessary for the analysis of all stereogenic units. Descriptors specified in digraphs may correspond to the final descriptors or to temporary (auxiliary) descriptors used only for ranking ligands and never appearing as final descriptors.

Generation of auxiliary descriptors must start from highest sphere, toward to root. In this way, all auxiliary descriptors in higher spheres than the one being determined are already assigned. This is sufficient, as the descriptor for an auxiliary center does not depend upon any descriptor between it and the root, as the priority of a ligand leading back to the digraph root will always be ranked by Rule 1a, with no need to consider auxiliary centers. This postulate follows from the fact that auxiliary centers are always offset from the root of a digraph, and so the path back to the root is always unique in connectivity and atomic numbers.

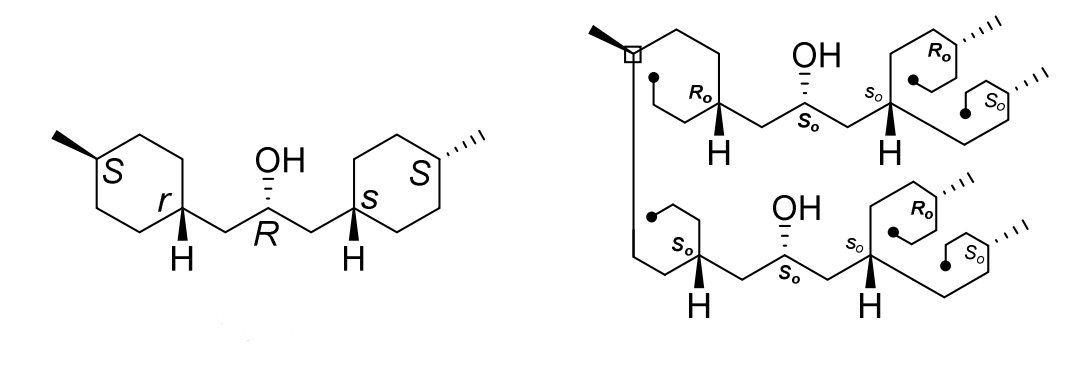
Pseudoasymmetry

Stereogenic units are called pseudoasymmetric (center, axis or plane) when they have distinguishable ligands ‘a’, ‘b’, ‘c’, ‘d’, two and only two of which are nonsuperposable mirror images of each other (enantiomorphic). Reflection of pseudoasymmetric centers is superimposable. These enantiomorphic ligands are represented by ‘╒ and ╕’ as designated by Prelog and Helmchen. The ‘r/s’ and ‘m/p’ stereodescriptors describing a pseudoasymmetric stereogenic unit are invariant on reflection in a mirror (for example ‘r’ remains ‘r’, and ‘s’ remains ‘s’), but are reversed by the exchange of any two ligands (‘r’ becomes ‘s’, and ‘s’ becomes ‘r’). Lower case stereodescriptors are used to describe pseudoasymmetric stereogenic units. Only when Rule 5 has been used, a pesuodommetric descriptor can be assigned because Rule 5 do a final check for enantiomorphic ligands.

Sequence rules

Rule 1a

Higher atomic number precedes lower.
Rule 1a is simple to understand, except for the special cases(mancude ring or rings systems), when a duplicate atom is involved in multiple resonance structures, a average atomic number of it should be used. It is sad to have to say that averaging the atomic number is a difficult procedure to describe, and there are not exact definitions for how to apply it. BB 2013 only mentioned several simple examples, such as benzene, pyridine or cyclopentadienyl anion. Without averaging atomic number in the Rule 1a, bellow two chemically equivalent Kekulé structures give different assignments at the stereocenter.

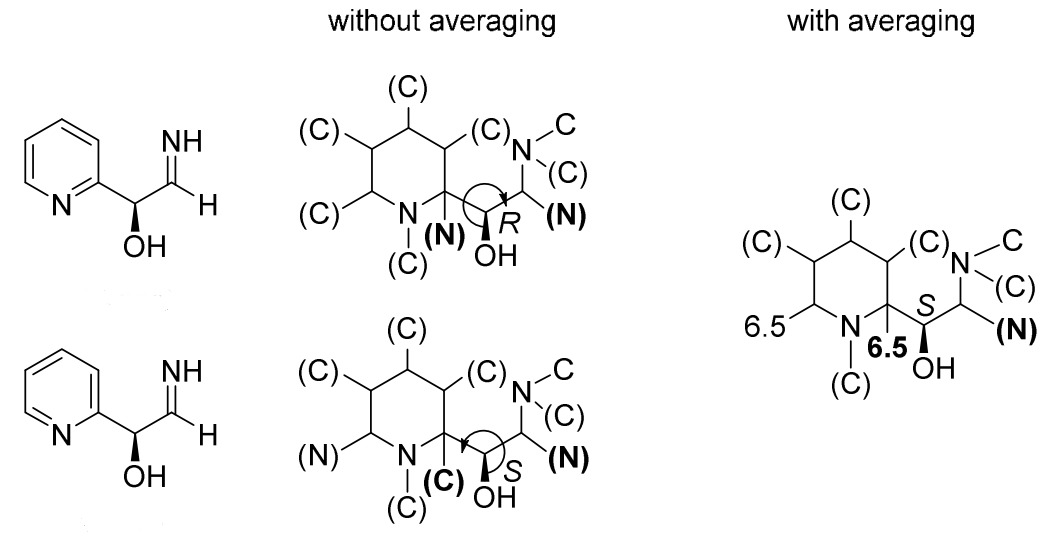
Rule 1b

A duplicate atom node whose corresponding nonduplicated atom node is the root or is closer to the root ranks higher than a duplicate atom node whose corresponding nonduplicated atom node is farther from the root.
Rule 1b is not sufficient.The problem is that although Rule 1b was designed to solve a problem with ring-closure duplicate nodes, the rule as stated also applies to multiple-bond duplicate nodes and Kekulé structure. To avoid this problem, a revision of Rule 1b is to assign to a multiple-bond duplicate node the distance to the root of its corresponding attached atom, not its corresponding duplicated atom.

Rule 2

Higher atomic mass number precedes lower.
Rule 2 is also not sufficient. When e one atom has an isotope indicated and one does not, and also (again) when several alternative Kekulé structures are involved. The problem is that “mass number” is always an integer -- the sum of the number of protons and neutrons in the nucleus, and can't calculate the mass number of a natural composition for the element. How to deal with this issue, where the term “mass number” is replaced with “atomic mass”. BB 2013 also mention that using atomic mass to arrange the ligands, an example is in BB 2013 Section P-92.3, it consider I precedes I¹²⁵.

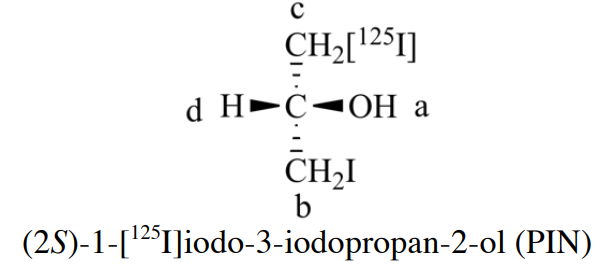
Rule 3

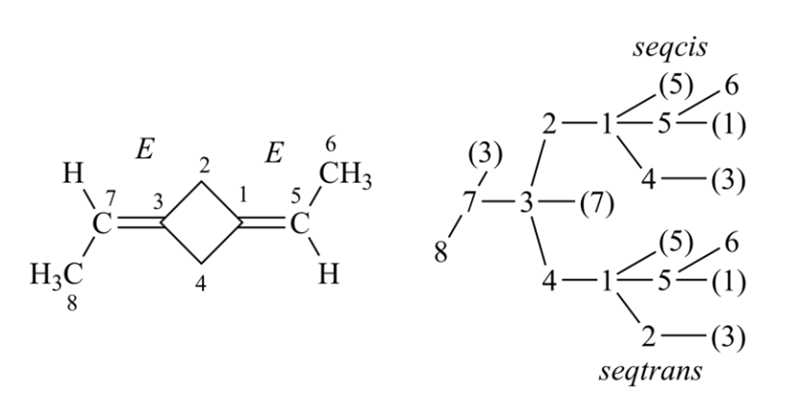
When considering double bonds and planar tetraligand atoms ‘seqcis’ = ‘Z’ precedes ‘seqtrans’ = ‘E’ and this precedes nonstereogenic double bonds.
The descriptors ‘E’ and ‘Z’ are used to describe ‘cis/trans-isomers’ at diastereomorphic double bonds. The application of Rule 3 leads to the specification of the configuration of compounds containing sets of ‘cis’ and ‘trans’ double bonds when the direct application of Sequence Rules 1 or 2 does not permit a conclusion to be reached. Auxiliary stereodescriptors are used when direct assignment of configuration cannot be made to double bonds, so before applying Rule 3 all auxiliary descriptors should be labeled. Placement of Rule 3 before Rule 4a ensures that only enantiomorphic (seqCis and seqTrans) comparisons involving double-bonds and cumulenes with an odd number of double bonds are left to consider in Rules 4 and 5.

Rule 4a

Chiral stereogenic units precede pseudoasymmetric stereogenic units and these precede nonstereogenic units.
Rule 4a is, (R or S) > (r or s), (M or P) > (m or p), and (seqCis or seqTrans) > (seqcis or seqtrans), and that all of these have higher priority than digraph nodes with no auxiliary descriptor. The purpose of Rule 4a is to ensure that all comparisons in Rule 4b and later are of the same general type:: R vs. S, M vs. P, or seqCis vs. seqTrans in Rules 4b; r vs s or m vs. p in Rule 4c; R vs. S or M vs. P in Rule 5. In addition, application of Rule 4a guarantees that the lists of ranked descriptors that are being compared in Rule 4b are of equal length.

Rule 4b

When two ligands have different descriptor pairs, then the one with the first chosen like descriptor pairs has priority over the one with a corresponding unlike descriptor pair.

Like descriptor pairs are: ‘RR’, ‘SS’
Unlike descriptor pairs are: ‘RS’, ‘SR’

Rule 4b is by far the most difficult rule to comprehend and implement. A new methodology has recently been described by Mata and Lobo to replace that described by Prelog and Helmchen. The rule for pairing stereodescriptors is as follows: A reference descriptor for chirality centers, identified as R or S (not associated with any node of the digraph and designated here with a bold font, for example, any of R, M, or secqCis can be assigned R for the purpose of processing Rules 4b), is chosen in each ligand and is:

the one associated with the highest rank node corresponding to a chiral unit in the ligand;
the one that occurs the most in the set of equivalent highest rank nodes; or
sequentially both descriptors (R and S), if these occur in the same number in the set of equivalent highest ranked nodes:
(i) If the number of reference descriptors is different in both ligands then the ligand with one reference descriptor has priority over the ligand with two reference descriptors;
(ii) If both ligands have the same number of reference descriptors, then the reference descriptor is paired with each one of the descriptors, identified as R or S, associated with nodes corresponding to chiral units, respecting their connectivity and hierarchy in the digraph.

In this way, all discussion can be expressed in terms of “equal” or “not equal” to a reference R or S, rather than “like” vs. “unlike”. When assigning seqCis/seqTrans and M/P auxiliary descriptors, which involve multiple atoms, it is critical that an implementation assign those descriptors to the node that is closest to the root. Otherwise the second phase of Rule 4b may fail.

The application of Rule 4b is more complex than previous rules, and it can be divided into three steps. First, ligands are ranked by Rule 1 - 4a, and choose reference descriptors for ligands. Second, using reference descriptors re-rank the nodes in a way that may cross digraph branches, and the hierarchy used in the comparison of the pairs of descriptors is established. Third, the nodes are scanned in rank order for auxiliary descriptor similarity to reference descriptors.

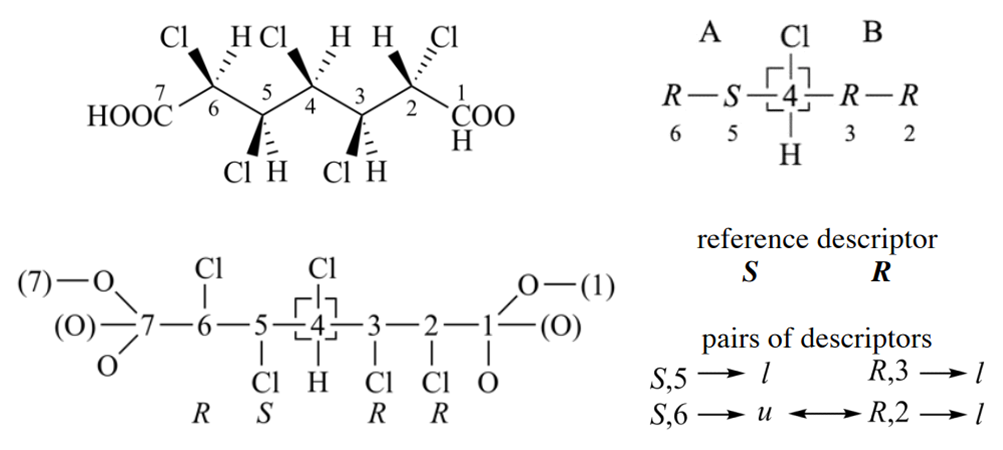
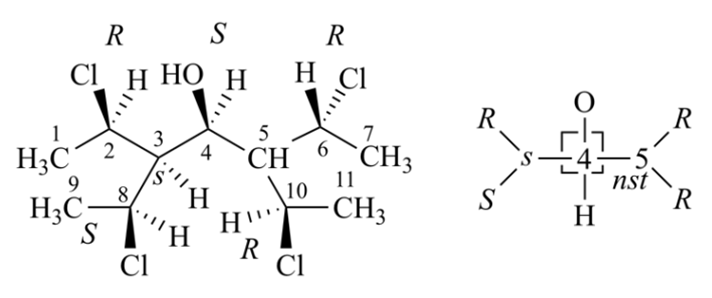
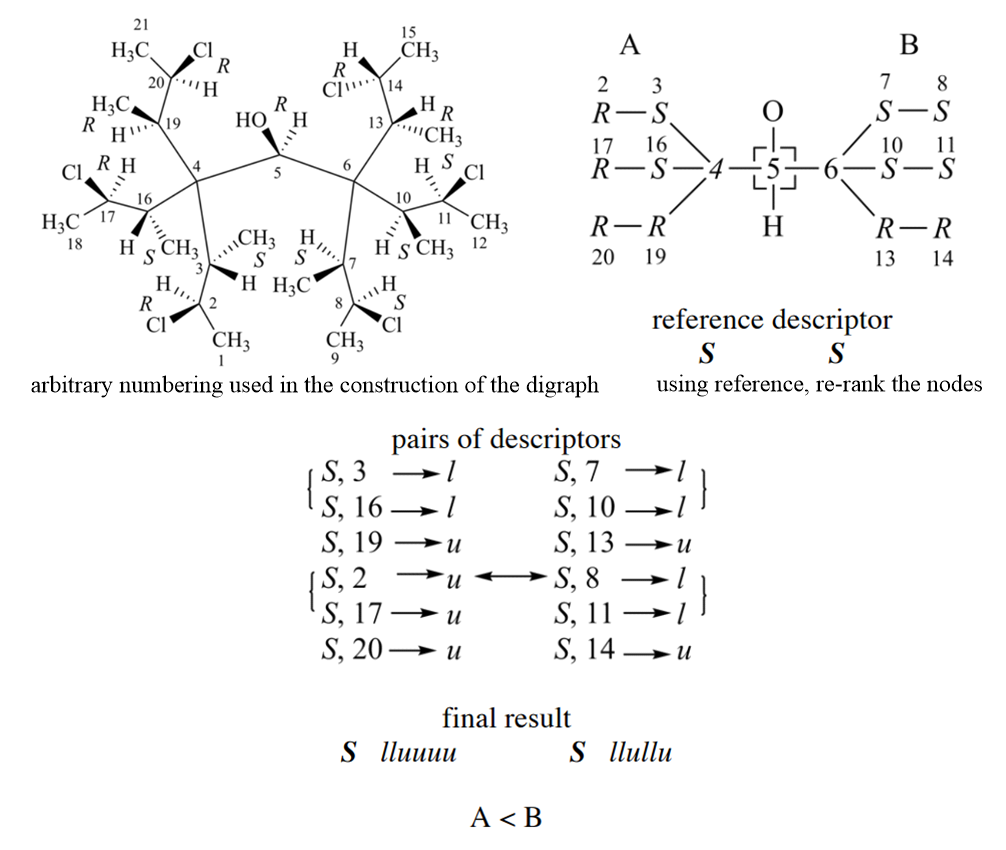
Follow is an example for criterion 2, it is more complex than above case. For branch A, three child nodes of 4 in sphere II are equivalent, two of them are ‘S’ and the other is ‘R’. Thus, the reference descriptor is ‘S’; it is the one that occurs most in the set of equivalent highest ranked nodes. Similarly, in the right branch the reference descriptor is ‘S’. The hierarchy used in the comparison of the pairs of descriptors is established as follows. After reordering the three nodes in sphere II of the digraph (nodes bonded to ‘C-4’ in the left branch and to ‘C-6’ in the right branch), the nodes are no more equivalent. Those that form like pairs have precedence over the one that forms an unlike pair. Similarly, the ranking in branch B gives precedence to like pairs.

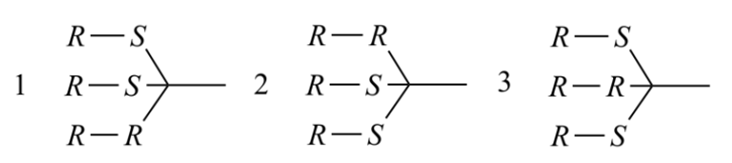
The reordering of the digraph is always required when applying the Sequence Rules. Before comparison according to Sequence Rule 4b, partial digraphs 1, 2, and 3 below (nodes at top of the digraph are equivalent or higher ranked than those nodes closer to the bottom of the digraph) are all valid to represent branch A. However, after comparison of sphere II only digraph 1 represents the hierarchy of the nodes.

Rule 4c

‘r’ precedes ‘s’ and ‘m’ precedes ‘p’.
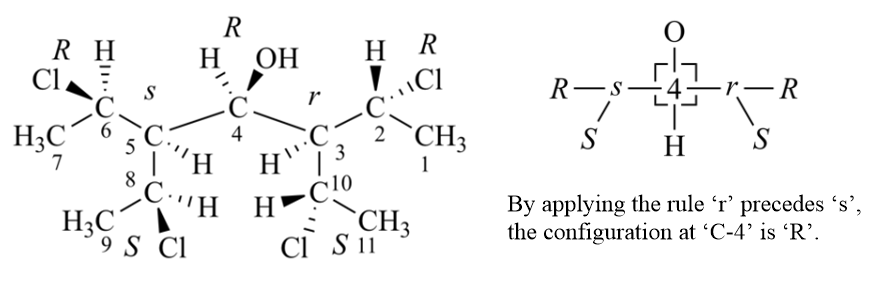
If the use of Rules 4b does not decide the ranking of all ligands of a stereogenic unit, it means that there are only three possibilities: (1) There is no ligand chirality; (2) two or more ligands have identical chirality descriptors; or (3) the two ligands each have sub-branches with opposite chirality. Rule 4c takes care of case (3), where we assign r over s, and m over p.

Rule 5

An atom or group with descriptor ‘R’, ‘M’, and ‘seqCis’ has priority over its enantiomorph ‘S’, ‘P’ or ‘seqTrans’.
Rule 5 does a final check for enantiomorphic ligands. If all ligands are finally distinguished after application of Rule 5, an additional test should be done to count the number of pairs of enantiomorphic ligands. The final descriptor will be r/s, m/p, or, in the case of akenes, seqCis/seqTrans, if and only if this number is one, otherwise it will be R/S, M/P, or seqcis/seqtrans (Z/E).

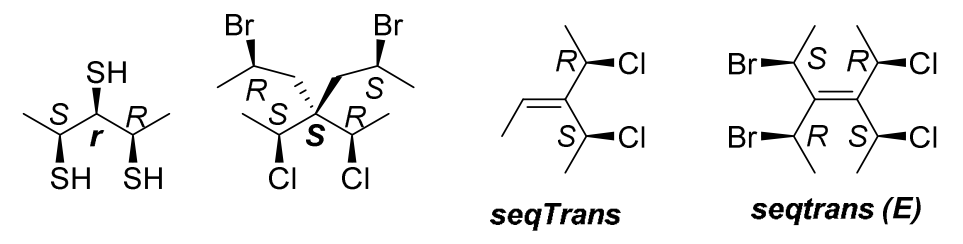
A simple way of using Rule 5 is that using both R and S reference descriptors, then comparing like/unlike sequences with R descriptor and S descriptor respectively, if there is an odd number of pairs that reverses priority, two ligands of pair are enantiomorphic, otherwise they are diasteromorphic. In the procedure of Rule 5, can't directly use the lists generated when using Rule 4b, new pair lists should be detected, because priorities may have changed after application of Rule 4c.

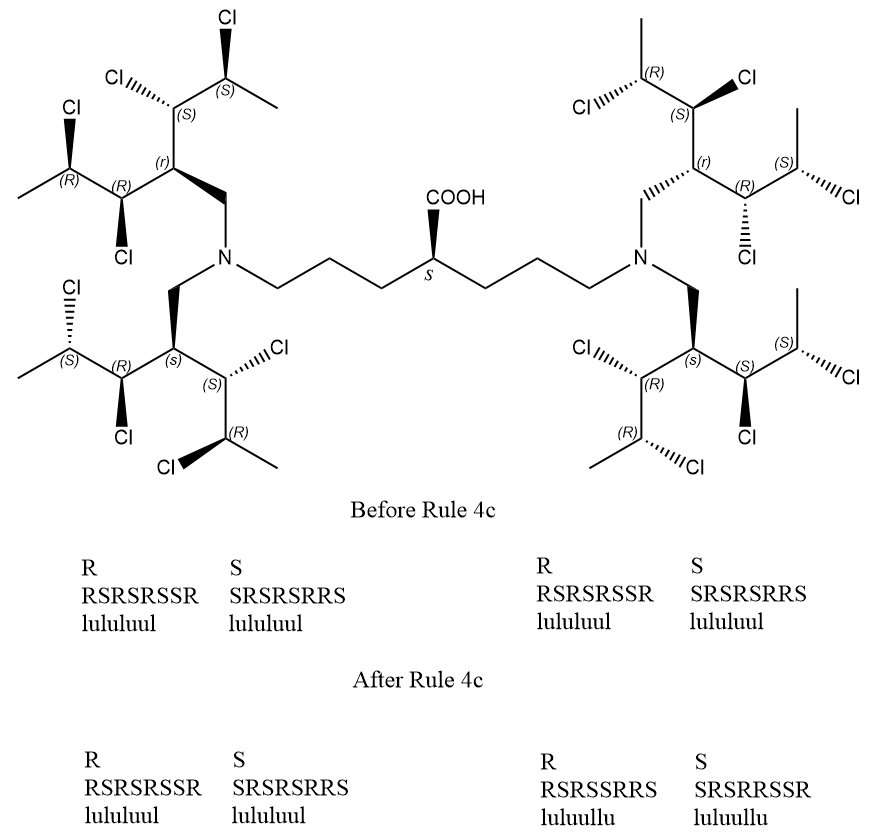
Above is a more complex example for Rule 5, the pair lists are equal in the procedure of Rule 4b, so ligands can't be distinguished by Rule 4b. After application of Rule 4c, the priorities of ligands are changed, new lists are generated in the procedure of Rule 5, and the right-hand ligand has higher priority for both R-reference and S-reference, therefore these two ligands are diasteromorphic, the stereogenic unit is asymmetric, and the ultimate descriptor will be S, not s.

Rule 6 (proposed)

An undifferentiated reference node has priority over any other undifferentiated node
Early on in the development of the CIP System, the key paper (the original idea of Rule 6 is also come from it, see reference 4) has mentioned that for C₂, D₂, C₃ and S₄ symmetry compounds, it need additional consideration to assign the stereo descriptors. But there is no a standard CIP rule to handle these compounds, only simple spiro structure is mentioned in BB 2013. So Rule 6 was proposed by Hanson et al in 2018, and it can take care of all these cases.

After application of Rule 5, if there are two or three or four pairs of identical ligands, Rule 6 can be applied. The solution for all such cases is simply to select one node of any one of the undistinguished ligands for promotion to higher rank. Basically, by arbitrarily breaking the symmetry in this way, the problem is immediately resolved upon inspection of the digraph.

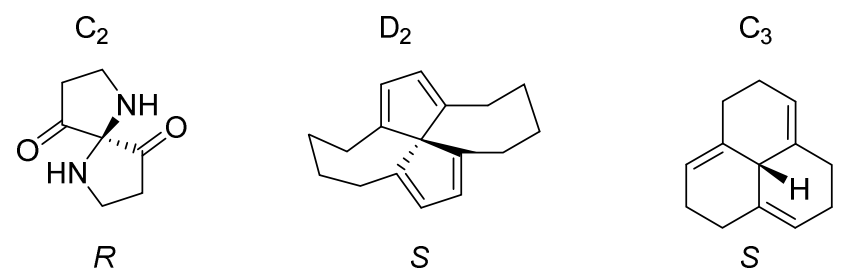
Bellow is two examples of the analysis of compounds by Rule 6, which sets Node 1 to be higher priority than Node 2. This single change decides also the priority 3 > 4, due to the presence of a ring connection from Node 3 back to Node 1 and from Node 4 back to Node 2.

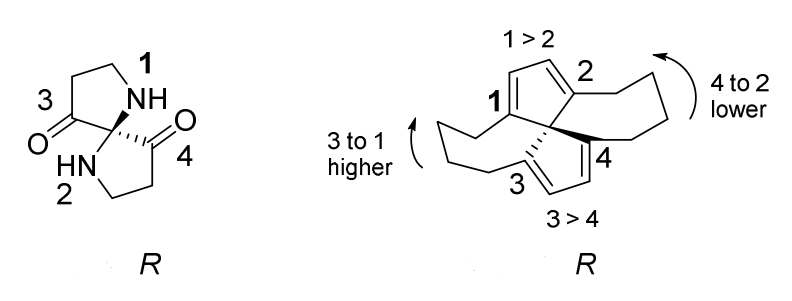
After application of Rule 6, there two possibilities: (a) There are still two undistinguished ligands. Such will be the case, for example, with simple acyclic compounds, such as CH2Cl2 or CHCl3. The center remains without descriptor. (b) All ligands are distinguished. The center receives a descriptor. Such will be the case only for compounds that have rings that involve the root atom and three or more ligands. A full application of Rule 6 tests all possible promotions, though this is necessary only for certain symmetries. Any matching R and S pairs are ignored; if a descriptor remains, it is valid.

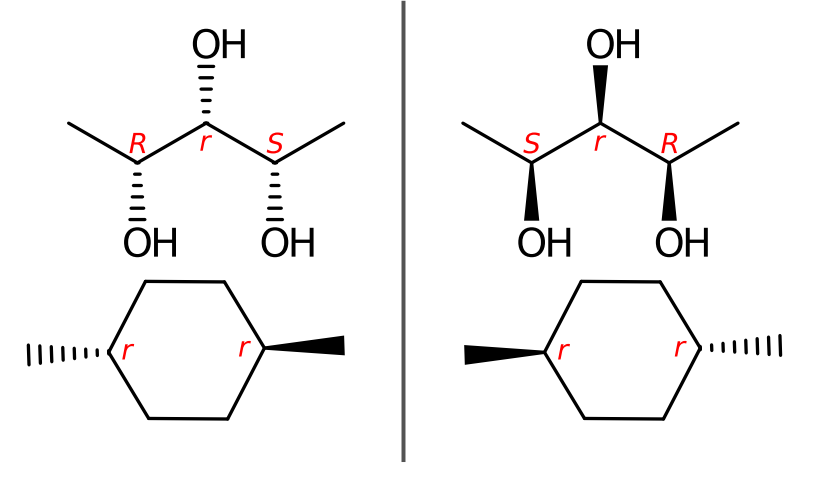
Incompleteness of CIP priority system

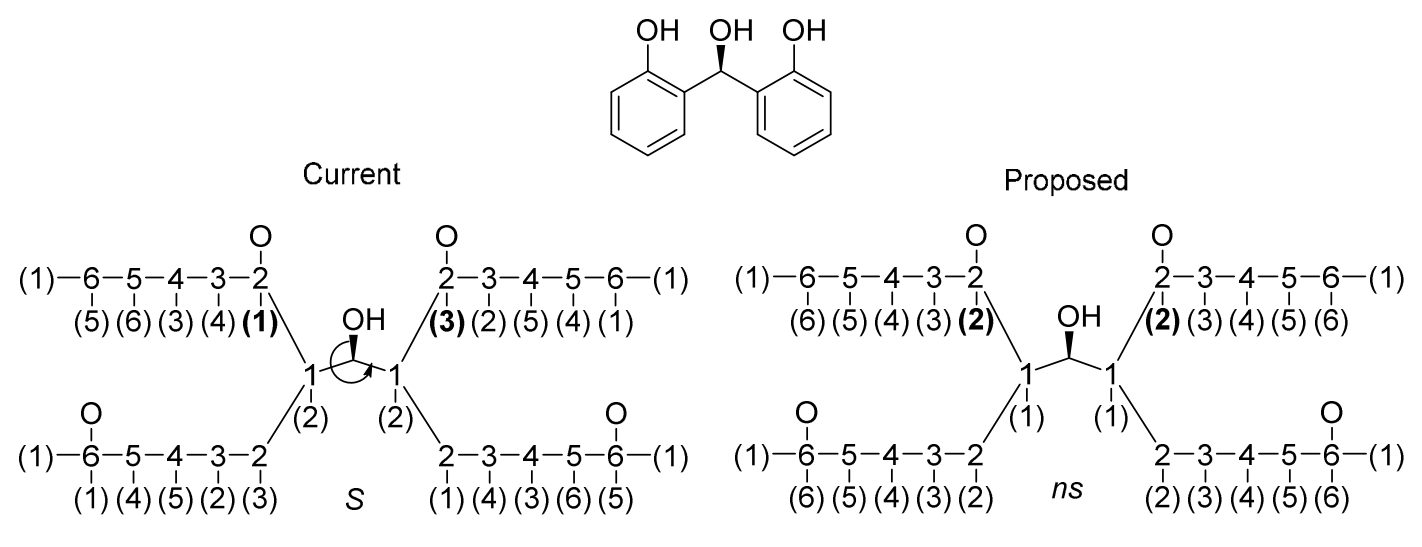
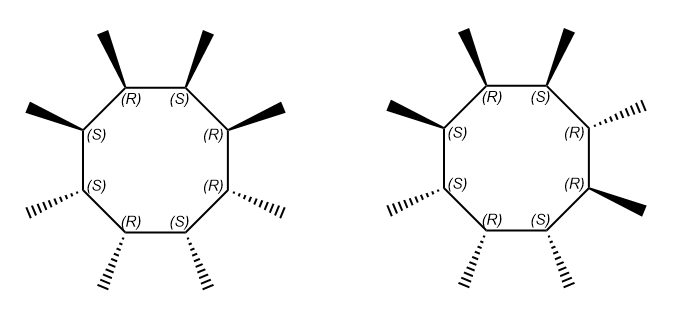
Although many efforts have been made to revise the CIP priority system, CIP priority system can't capture all stereochemistry differences, for some special cases. The reconstruction problem affects the use of CIP descriptors for unique naming. The distribution of CIP descriptor labels of bellow two compounds are identical although the molecules have different configurations. For homo-substituted cycloalkanes, the number of such ambiguities usually increases with ring size starting at size eight.

Software

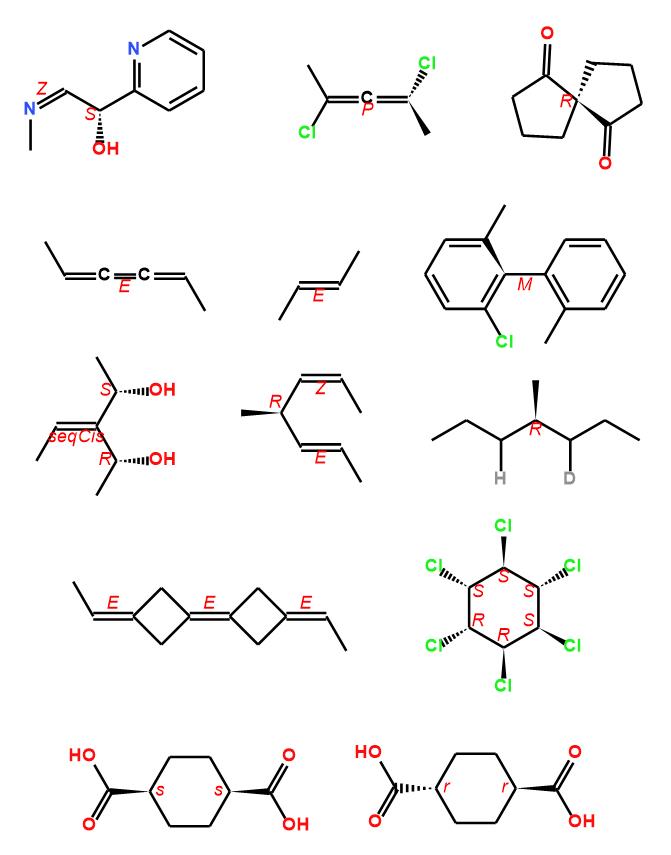
There are many softwares can detect the CIP descriptors of chiral compounds, such as ACD/ChemSketch, MarvinSketch, ChemDraw, Biovia Draw, RDKit, Indigo, Centres. John Mayfield et al. have done a comparison for these software, more details can get from reference 3. A full rules implement is also included in Ferrocene, bellow examples are generated by Ferrocene CIP detection, anyone is interested in it, can try it on this page.